https://www.acmicpc.net/problem/14938

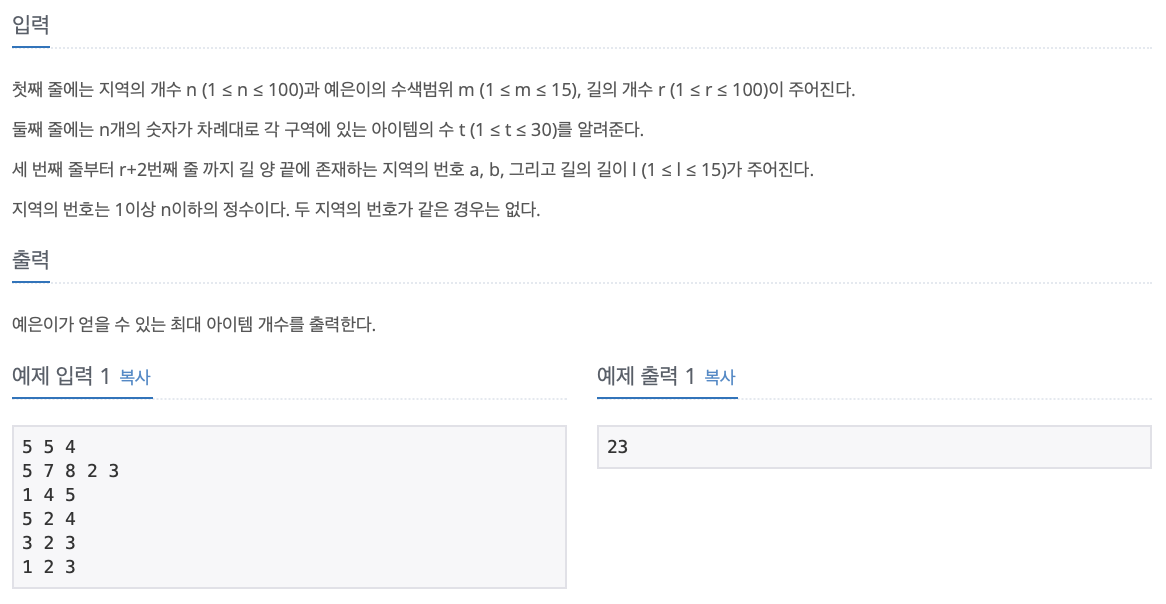
노드들 간의 최소 거리를 구한 다음, 노드를 하나씩 탐색해 수색 범위 내에서 얻을 수 있는 아이템 개수를 구하고, 개수가 최대인 경우를 출력하는 문제입니다. 이는 플로이드-워셜(Floyd-Warshall) 알고리즘을 이용하면 됩니다. 저번 글에 썼던 문제와 같은 알고리즘을 사용하기에 수색 범위와 아이템 개념만 추가해주면 됩니다. 플로이드-워셜 알고리즘에 대한 설명을 지난 글에 아주 간단히 적었습니다.
https://yjs2673.tistory.com/23
/<> 백준 11404번 : 플로이드 (C언어) - 모나오랭의 개발일지
https://www.acmicpc.net/problem/11404 그래프 문제 중 플로이드-워셜(Floyd-Warshall) 알고리즘을 사용하는 문제입니다. 플로이드-워셜 알고리즘은 한 노드가 다른 노드에게 도달하는 데 걸리는 최소 비용(
yjs2673.tistory.com
1. 지역과 길의 개수, 거리를 저장하는 배열을 생성합니다
2. 지역마다 존재하는 아이템 개수를 저장한는 배열을 생성합니다.
3. 플로이드-워셜 알고리즘을 이용해 지역과 지역 사이의 거리를 최소로 바꿉니다.
4. 지역을 하나씩 탐색해 수색 범위 내에서 얻을 수 있는 아이템 개수를 구합니다.
5. 최대로 구할 수 있는 아이템 개수를 출력합니다.
<코드>
#include <stdio.h>
#define inf 987654321
int n, m, r;
int cost[101][101] = {0, };
int item[101] = {0, };
int max = 0;
void floyd_warshall() {
for(int k = 1; k <= n; k++) {
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(cost[i][j] > cost[i][k] + cost[k][j]) cost[i][j] = cost[i][k] + cost[k][j];
}
}
}
}
void check() {
for(int i = 1; i <= n; i++) {
int total_item = item[i];
for(int j = 1; j <= n; j++) {
if(i != j && cost[i][j] <= m) total_item += item[j];
}
if(max < total_item) max = total_item;
}
}
int main() {
scanf("%d %d %d", &n, &m, &r);
for(int i = 1; i <= n; i++) {
for(int j = 1; j <= n; j++) {
if(i == j) cost[i][j] = 0;
else cost[i][j] = inf;
}
}
for(int i = 1; i <= n; i++) scanf("%d", &item[i]);
for(int i = 0; i < r; i++) {
int u, v, c;
scanf("%d %d %d", &u, &v, &c);
cost[u][v] = c;
cost[v][u] = c;
}
floyd_warshall();
check();
printf("%d\n", max);
return 0;
}
데이크스트라(Dijkstra) 알고리즘으로 풀 수도 있는데, 모든 지역 간의 최소 거리를 구해야 하므로 결국 데이크스트라를 n번 돌려야 하기 때문에 시간 복잡도는 똑같이 O(n^3)입니다. 게다가 데이크스트라는 거리가 음수인 경우 사용할 수 없으므로(문제 조건엔 없음) 더 용이한 플로이드-워셜로 풀었습니다. 그래프 문제를 풀면서 데이크스트라, 플로이드-워셜 알고리즘에 더 친숙해지고 있습니다. BFS DFS와 더불어 중요한 탐색 알고리즘이므로 자주 복습해야겠습니다.
'백준' 카테고리의 다른 글
| /<> 백준 2579번 : 계단 오르기 (C언어) (1) | 2024.08.17 |
|---|---|
| /<> 백준 17219번 : 비밀번호 찾기 (C언어) (0) | 2024.08.17 |
| /<> 백준 11404번 : 플로이드 (C언어) (0) | 2024.08.07 |
| /<> 백준 1021번 : 회전하는 큐 (C언어) (1) | 2024.08.04 |
| /<> 백준 1331번 : 나이트 투어 (C언어) (0) | 2024.08.04 |